Quantum Computing Files: Tuesday's Edition
Quantum Computing Files: a newsletter about Quantum.
Welcome back to the Quantum Computing Files. This is the third post edition of this newsletter about Quantum Technologies. A Tuesday edition.
I will be posting on Quantum Computing Files twice a week, with occasional schedule changes or missing posts due to other priority committments/issues being in due course announced. I will try to publish resources and links about Quantum Computing techologies/science I find within my own remit, trying to be realist about the scope of what I can provide, but also confident about the relevance or significance of what this newsletter content can accomplish. Each edition will strive to be contained in terms of resources provided, giving the reader/audience the necessary time to digest it and think about it. This is a thought enhancement newsletter, not a bag full of negleted links…!
Suggestions are welcomed as well as new subscriptions and sharings! Let’s go along for the excitement - great - of Quantum Physics Technologies!
A Research Paper:
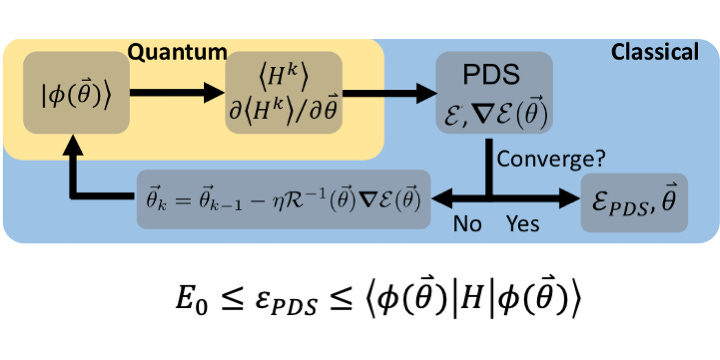
Variational quantum solver employing the PDS energy functional (Quantum Journal - June 10th)
Abstract:
Recently a new class of quantum algorithms that are based on the quantum computation of the connected moment expansion has been reported to find the ground and excited state energies. In particular, the Peeters-Devreese-Soldatov (PDS) formulation is found variational and bearing the potential for further combining with the existing variational quantum infrastructure. Here we find that the PDS formulation can be considered as a new energy functional of which the PDS energy gradient can be employed in a conventional variational quantum solver. In comparison with the usual variational quantum eigensolver (VQE) and the original static PDS approach, this new variational quantum solver offers an effective approach to navigate the dynamics to be free from getting trapped in the local minima that refer to different states, and achieve high accuracy at finding the ground state and its energy through the rotation of the trial wave function of modest quality, thus improves the accuracy and efficiency of the quantum simulation. We demonstrate the performance of the proposed variational quantum solver for toy models, H22 molecule, and strongly correlated planar H44 system in some challenging situations. In all the case studies, the proposed variational quantum approach outperforms the usual VQE and static PDS calculations even at the lowest order. We also discuss the limitations of the proposed approach and its preliminary execution for model Hamiltonian on the NISQ device.
Conclusion
In summary, we propose a new variational quantum solver that employs the PDS energy gradient. In comparison with the usual VQE, the PDS(K)-VQS helps identify an upper bound energy surface for the ground state, and thus frees the dynamics from being trapped at local minima that refer to non-ground states. In comparison with the static PDS(K) expansions, the PDS(K)-VQS guides the rotation of the trial wave function of modest quality, and is able to achieve high accuracy at the expense of low order PDS(K) expansions.
An Interesting Link from a Website:
Quantum Breakthrough: New Invention Keeps Qubits of Light Stable at Room Temperature (SciTechDaily - June 17th)
Researchers from University of Copenhagen have developed a new technique that keeps quantum bits of light stable at room temperature instead of only working at -270 degrees. Their discovery saves power and money and is a breakthrough in quantum research.
Single photons or qubits of light, as they are also called, are extremely difficult to hack.
However, in order for these qubits of light to be stable and work properly they need to be stored at temperatures close to absolute zero — that is minus 270 C — something that requires huge amounts of power and resources.
Yet in a recently published study, researchers from University of Copenhagen, demonstrate a new way to store these qubits at room temperature for a hundred times longer than ever shown before.
“We have developed a special coating for our memory chips that helps the quantum bits of light to be identical and stable while being in room temperature. In addition, our new method enables us to store the qubits for a much longer time, which is milliseconds instead of microseconds — something that has not been possible before. We are really excited about it,” says Eugene Simon Polzik, professor in quantum optics at the Niels Bohr Institute.
The special coating of the memory chips makes it much easier to store the qubits of light without big freezers, which are troublesome to operate and require a lot of power.
Therefore, the new invention will be cheaper and more compatible with the demands of the industry in the future.
Reference: “Room-temperature single-photon source with near-millisecond built-in memory” by Karsten B. Dideriksen, Rebecca Schmieg, Michael Zugenmaier and Eugene S. Polzik, 17 June 2021, Nature Communications.
DOI: 10.1038/s41467-021-24033-8
A Quantum Video to Watch:
Quantum Error Correction with Non-Abelian Topological Codes | Seminar Series with Guanyu Zhu (Qiskit - June 18th)
Speaker: Guanyu Zhu
Host: Zlatko Minev, Ph.D.
Title: Quantum Error Correction with Non-Abelian Topological Codes
Abstract: The surface code is one of the most promising candidates to realize fault-tolerant quantum computation in the near term. However, a large overhead exists due to the need of magic state distillation. An alternative approach is resroting to non-Abelian topological codes which can perform universal quantum computing via braiding non-Abelian anyons in two spatial dimension. In this talk, we consider a two-dimensional quantum memory of qubits which realizes the non-Abelian Turaev-Viro code, and devise strategies for error correction when those qubits are subjected to depolarizing noise. Building on the concept of tube algebras from topological quantum field theory, we construct a set of measurements and of quantum gates which map arbitrary qubit errors to the string-net subspace and allow for the characterization of the resulting error syndrome in terms of doubled Fibonacci anyons. Tensor network techniques then allow to quantitatively study the action of Pauli noise on the string-net subspace. We perform Monte Carlo simulations of error correcting this Fibonacci code, and compare the performance of several decoders. For the case of a fixed-rate sampling depolarizing noise model, we find an error correction threshold of 4.7% using a clustering decoder. To the best of our knowledge, this is the first time that a threshold has been estimated for a two-dimensional error correcting code for which universal quantum computation can be performed within its code space via braiding anyons.